R 実験計画法を利用した要因分析

今回は、実験計画法による要因分析の方法について例を交えて紹介したい。

1.  分析の前提

まず、今回の例の設定を述べる。

マンション販売のコンサルタントとして、デベロッパーと協力してマンションの販売数を上げるために重要な要素を調査することになった。ちょうど、新しいマンションを建てる計画があり、10部屋までであれば実験のために要因を自分で決められることになった。販売数には以下の4つの要因が関係すると仮定する。

・部屋のレイアウト ("1LDK", "2LDK", "3K"),

・階層 ("low", "high"),

・部屋の方角 ("south", "east", "west"),

・和室or 洋室 ("wa", "yo")

全ての要因の組み合わせは、3×2×3×2 = 36 通りあり、実験の可能な10部屋を大きく超えている。Rでは、次のようにexpand.grid関数を用いて、全パターンのリストを作成することができる。

#Create list of partners
RoomFactors <- expand.grid(
 layout = c("1LDK", "2LDK", "3K"),
 Floor = c("low", "high"),
 Direction = c("south", "east", "west"),
 Wayo = c("wa", "yo")
)

結果、次のようなリストが作成された。

> RoomFactors
 layout Floor Direction Wayo
1 1LDK low south wa
2 2LDK low south wa
3 3K low south wa
4 1LDK high south wa
5 2LDK high south wa
6 3K high south wa
7 1LDK low east wa
8 2LDK low east wa
9 3K low east wa
10 1LDK high east wa
11 2LDK high east wa
12 3K high east wa
13 1LDK low west wa
14 2LDK low west wa
15 3K low west wa
16 1LDK high west wa
17 2LDK high west wa
18 3K high west wa
19 1LDK low south yo
20 2LDK low south yo
21 3K low south yo
22 1LDK high south yo
23 2LDK high south yo
24 3K high south yo
25 1LDK low east yo
26 2LDK low east yo
27 3K low east yo
28 1LDK high east yo
29 2LDK high east yo
30 3K high east yo
31 1LDK low west yo
32 2LDK low west yo
33 3K low west yo
34 1LDK high west yo
35 2LDK high west yo
36 3K high west yo

2. 直交表によるパターン数の削減

前述の36パターンのすべてを試すことになると、36部屋が必要となってしまう。また、36部屋のそれぞれに該当する部屋があるとも限らない。このようにパターン数が多く実験が出来ない場合は、直交表というものを使ってパターン数を削減することができる。直交表では、次のように「数独の構造」を作ってパターン数の削減を試みる。下記は64パターンを16パターンに削減する場合の直交表である。

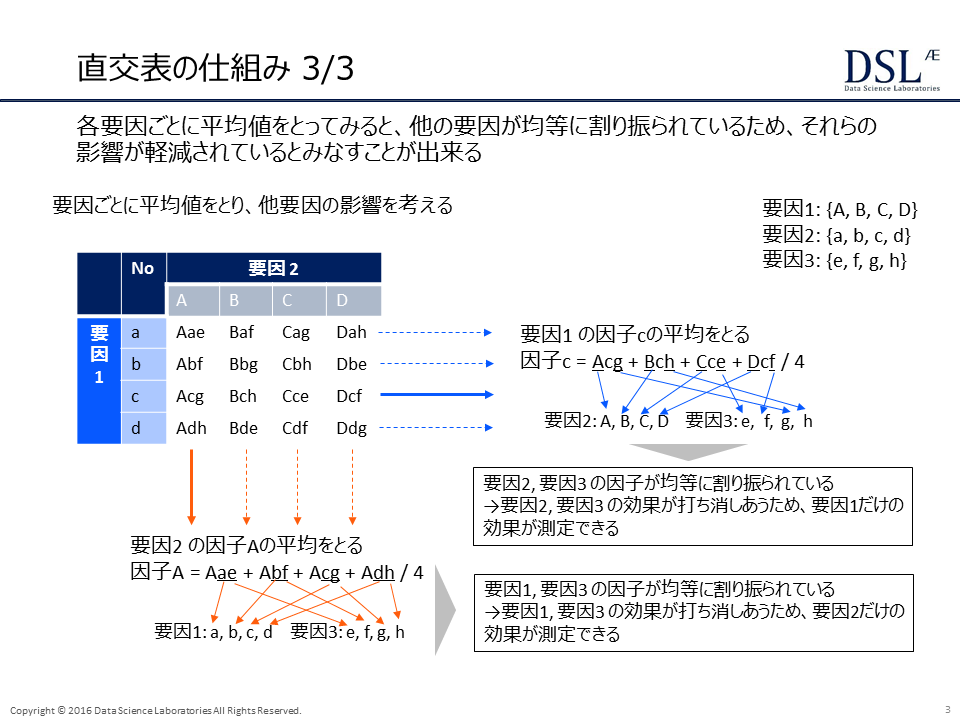
上記の図のように、各要因の平均を取ると、他の要因が均等に割り振られているためそれらの要素が軽減されているとみなすことができるのである。

しかし、直交表を作成するには、上記のようにパズル的なノウハウが必要である。しかし、Rのconjointパッケージに含まれるcaFactorialDesign関数を用いると直交表を作成した上でパターン数を削減することができる。

#Create orthogonal table
design_ort <- caFactorialDesign(data=RoomFactors, type="orthogonal")

"orthogonal"は「直角の」という意味である。結果はこちら。 

> design_ort
 layout Floor Direction Wayo
5 2LDK high south wa
12 3K high east wa
13 1LDK low west wa
21 3K low south yo
22 1LDK high south yo
26 2LDK low east yo
28 1LDK high east yo
35 2LDK high west yo
36 3K high west yo

36通りが、9通りまで削減されたことがわかる。したがって、実験に必要な部屋は9部屋で良い。

3. 実際にデータをとって、分散分析

上記の組み合わせを満たす９部屋（値段や広さ等の要因は同じ）の資料請求人数をポイントとして割り振ったところ、上から117,67,49,92,79,100,65,84,71となった。

この結果を元に分散分析を実施する。分散分析はaov関数を用いることで実施が出来る。

#Create dataframe for anova
V <- c(117,67,49,92,79,100,65,84,71)
dat <- cbind(design_ort,V)

####2. Four-way Anova####
result <- aov(V~., data=dat)
str(result)
summary(result)

結果は次の通り。

> summary(result)
 Df Sum Sq Mean Sq F value Pr(>F) 
layout 2 2008.2 1004.1 19.753 0.0482 *
Floor 1 0.1 0.1 0.001 0.9766 
Direction 2 1219.6 609.8 11.996 0.0769 .
Wayo 1 34.7 34.7 0.683 0.4954 
Residuals 2 101.7 50.8 
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

95%信頼区間でみると、部屋のレイアウト、90％信頼区間で   見ると部屋の方向が資料の請求人数に寄与していることがわかった。

【補足】分散分析とは、条件による違いで評価のバラつき（分散）がどの程度異なるかを検定することで、効果のある要因を見極める方法です。

4. まとめ

直交表を活用して分散分析を実施することで、実験回数を大きく減らすことができた。このように、実験回数に制約がある場合は実験計画法を実施することで効率的にある結果に対して寄与する要因を分析することができる。