今回は、下記サンプルデータを用いて商品開発における各要素の最適な組み合わせを見つけ出す方法を紹介したい。
1. 分析の前提
今回は、大手百貨店の商品企画部として、以下のシチュエーションで分析を行うこととする。ある大手百貨店の飲食店のテナントでお昼にお弁当を販売することになった。もっともよく売れるお弁当の中身を考えるため、各項目について以下の選択肢を定めた。
‐穀物:ご飯,麺
‐メインのおかず:ビーフ,フィッシュ,チキン
‐サブのおかず:ゆで卵,エビ,ソーセージ
‐野菜:オニオン,キャロット,ポテト
‐野菜の量:多い,普通,少ない
‐つけあわせ:チーズ,コーン,オリーブ
‐穀物の量:少な目,ふつう,大盛り
‐価格:350円,450円,550円
項目の組合せを決めて、常連のお客様にアンケートを行い、点数をつけて貰うことにする。
2. 直交表によるパターン数の削減
本来ならば、穀物、メイン、サブ、野菜、野菜の量、つけあわせ、穀物の量、価格の種類を勘案して、2×3×3×3×3×3×3=1,458種類の弁当を作る必要があるが、すべての組合せを設定するにはパターンが多すぎるのでL18直交表を使うことにする。
Rのconjointパッケージに含まれるcaFactorialDesign関数を用いると簡単に作成することができる。(※前記事参照)直交表を使った結果、1,458種類を以下の18通りに削減することができる。

各要因の平均を取ると、他の要因が均等に割り振られているためそれらの影響が軽減されているとみなすことができるためである(※前回記事参照)。このデータをを"8_L18_table.csv"、"8_levels.csv"というファイルに保存する。
"8_L18_table.csv"の内容
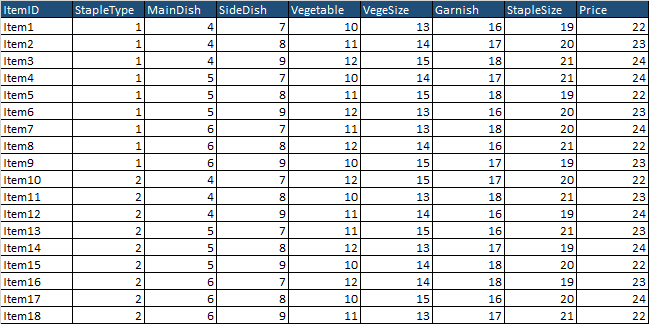
"8_levels.csv"の内容

"8_L18_table.csv"に掲載されている番号が、"8_levels.csv"に掲載されているラベルと対応していることに注意頂きたい。このようなデータとラベルを分けることは、Rでコンジョイント分析を行うConjoint関数を使う際に必要な処理なので覚えておくとよい。
3. コンジョイント分析
上記の直交表に対応するお弁当に対して、常連のお客様にアンケートを実施し、点数をつけてもらった。結果次のようなデータが収集された。(※:サンプルデータです)

アンケート回答者は、18種類の弁当に対してそれぞれ0,5,10点のいずれかの点数を付けている。上記データを"8_obento_data.csv"というファイルに保存する。その上で、以上のデータをRで読み込み、Conjoint関数でコンジョイント分析を行う。コードは次の通り。
####0. Package Install####
if("conjoint" %in% rownames(installed.packages()) == FALSE) {install.packages("conjoint")}
library(conjoint)
####1. Data Preparation####
###Data Input
##Quentionnaire data
dat <- read.csv("8_obento_data.csv", header=TRUE)
dim(dat) #Dimension of the data - 85 rows and 22 columns
str(dat) #Confirm data type of each column
dat_all <- dat[,-c(1:4)] #Erase demographic information
##Item list - orthogonal matrix
L18 <- read.csv("8_L18_table.csv", header=TRUE)
dim(L18) #Dimension of the data - 18 rows and 9 columns
str(L18) #Confirm data type of each column
L18 <- L18[,-1] #Erase ItemID
cor(L18) #Confirm orthogonality
##Factor information
attr <- read.csv("8_levels.csv", header=TRUE)
####2. Conjoint analysis for all data####
Conjoint(dat_all, L18, attr) #Conjoint analysis
title(main="Importance of Factors (all data)")
RでConjoint関数を使うと、次のような3種類のアウトプットが出力される。
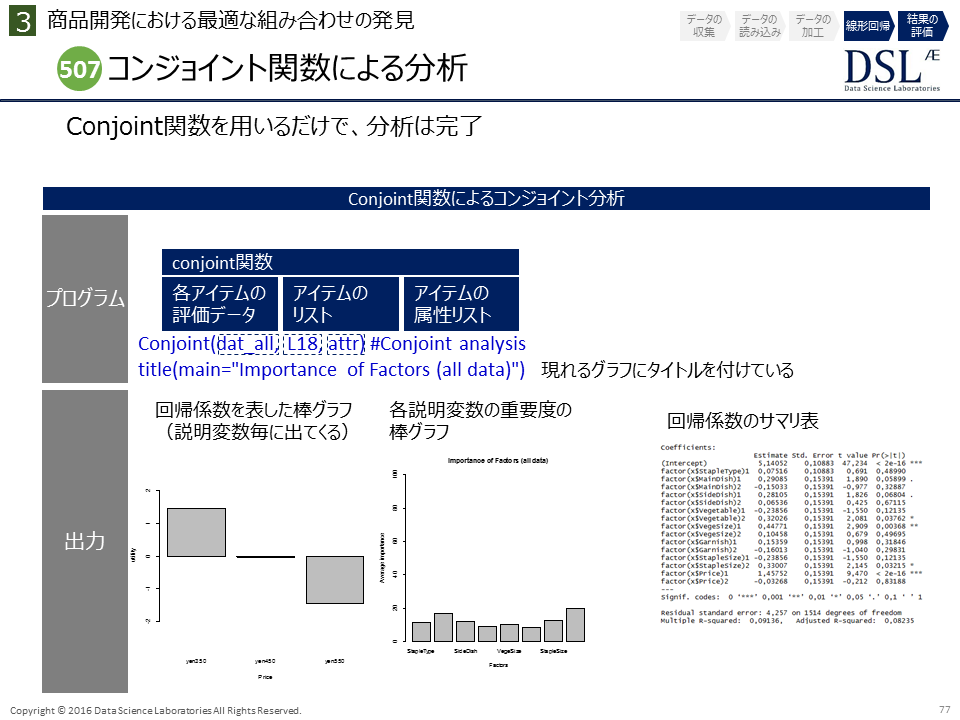
3.1 回帰係数を表す棒グラフ
各項目毎にグラフがたくさん出てくるが、解釈方法は簡単で、大きいプラスの値程、評価にはプラスになると考えれば良い。下記は一例である。

上記では野菜(vegetable)と穀物の量(Staple size)の2項目について示したが、他の項目についても同様である。
最も得点が高くなる組み合わせを見極めることで、最も評価が高くなる項目の組み合わせを導くことができる。

3.2 各説明変数の重要度の棒グラフ(寄与率の棒グラフ)
前述の「回帰係数を表す棒グラフ」に次いで登場するのが各説明変数の重要度の棒グラフである。各項目(説明変数)の寄与率(データの持つ情報を説明する割合)が表示される。
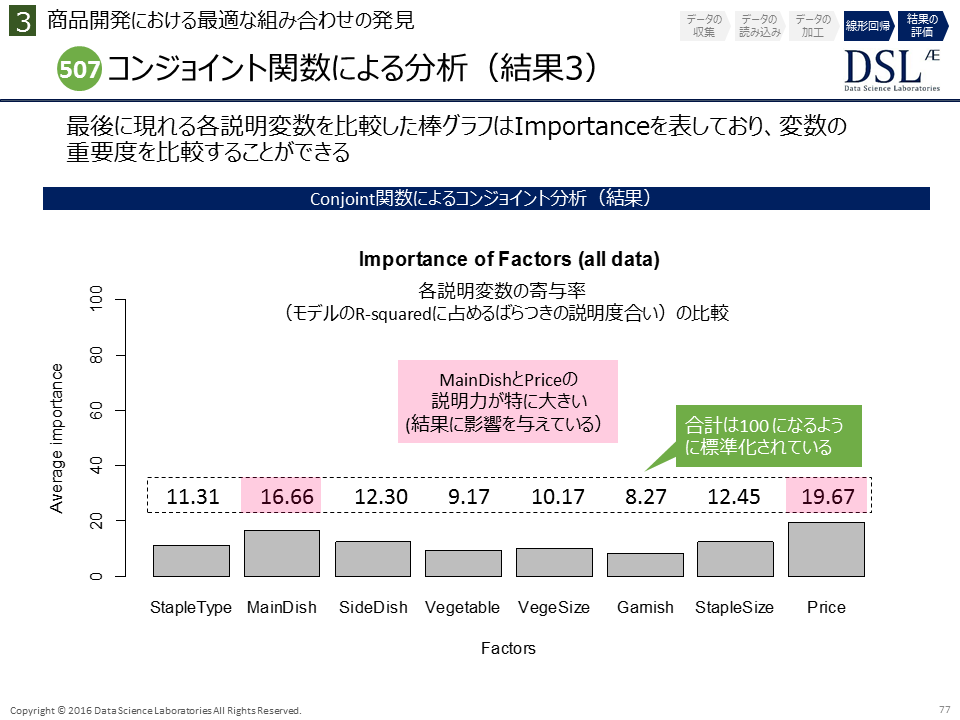
今回の場合は、MainDish(メインディッシュの種類)とPrice(価格)が評価に最も影響する2項目であることがわかる。
3.3 回帰係数のサマリ表
回帰係数等をサマリした表も現れる。係数の有意性を確認することができる。
Residuals:
Min 1Q Median 3Q Max
-8,0934 -3,4217 -0,1263 3,3965 7,1465
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5,265e+00 2,067e-01 25,469 < 2e-16 ***
factor(x$StapleType)1 -8,838e-02 2,067e-01 -0,428 0,6692
factor(x$MainDish)1 4,167e-01 2,924e-01 1,425 0,1549
factor(x$MainDish)2 -3,788e-02 2,924e-01 -0,130 0,8970
factor(x$SideDish)1 5,682e-01 2,924e-01 1,943 0,0527 .
factor(x$SideDish)2 -2,652e-01 2,924e-01 -0,907 0,3650
factor(x$Vegetable)1 -3,409e-01 2,924e-01 -1,166 0,2443
factor(x$Vegetable)2 2,273e-01 2,924e-01 0,777 0,4374
factor(x$VegeSize)1 3,409e-01 2,924e-01 1,166 0,2443
factor(x$VegeSize)2 -1,136e-01 2,924e-01 -0,389 0,6977
factor(x$Garnish)1 4,545e-01 2,924e-01 1,555 0,1208
factor(x$Garnish)2 -3,458e-16 2,924e-01 0,000 1,0000
factor(x$StapleSize)1 -1,894e-01 2,924e-01 -0,648 0,5175
factor(x$StapleSize)2 1,515e-01 2,924e-01 0,518 0,6046
factor(x$Price)1 1,667e+00 2,924e-01 5,701 2,4e-08 ***
factor(x$Price)2 2,273e-01 2,924e-01 0,777 0,4374
---
Signif. codes: 0 ‘***’ 0,001 ‘**’ 0,01 ‘*’ 0,05 ‘.’ 0,1 ‘ ’ 1
Residual standard error: 4,114 on 380 degrees of freedom
Multiple R-squared: 0,1422, Adjusted R-squared: 0,1084
F-statistic: 4,201 on 15 and 380 DF, p-value: 3,35e-07
4. 属性別の分析
今回のデータでは、男女や年齢、弁当の購入頻度についてのデータも存在するため、これらの区分別のコンジョイント分析も実施できる。
4.1 男女別の分析
男性と女性をそれぞれ分析するため、for文を使って、男性、女性の順番で分析することにする。
####3. Conjoint analysis by segment####
##Conjoint analysis by gender
sexs = c("Male", "Female")
for (i in 1:max(dat$Sex)) {
dat_p <- subset(dat, Sex==i) #Extract each gender from all data
if (nrow(dat_p) < 20) next #If number of rows is less than 20, skip the factor
dat_p <- dat_p[,-c(1:4)] #Delete demographic columns(ID, Sex, Age, Frequency)
Conjoint(dat_p, L18, attr) #Conjoint analysis
titleName = paste("Importance of Factors (", sexs[i], ")")
title(main=titleName) #Add barplot title
Sys.sleep(5) #Stop program for 5 seconds
}
男性の場合の寄与率の棒グラフはこちら。
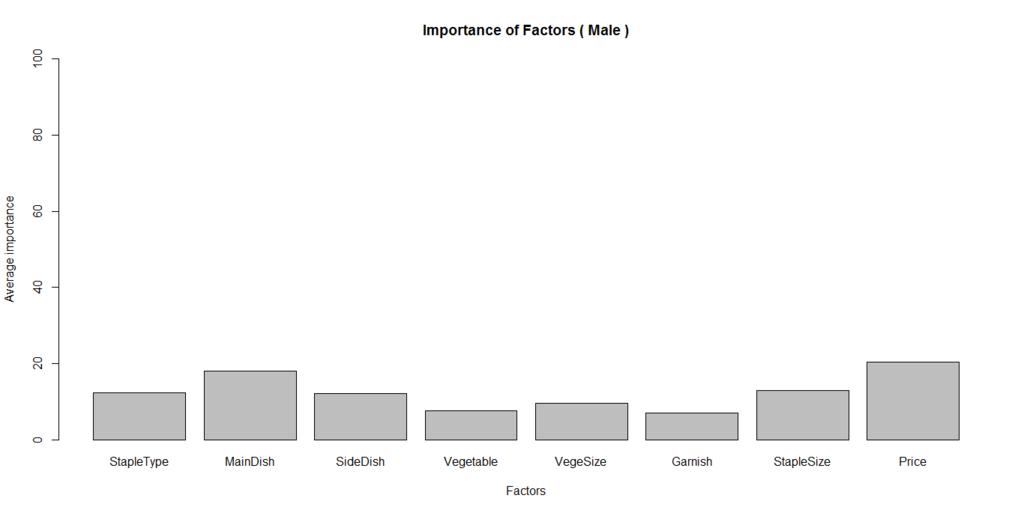
女性の場合の寄与率のグラフはこちら。
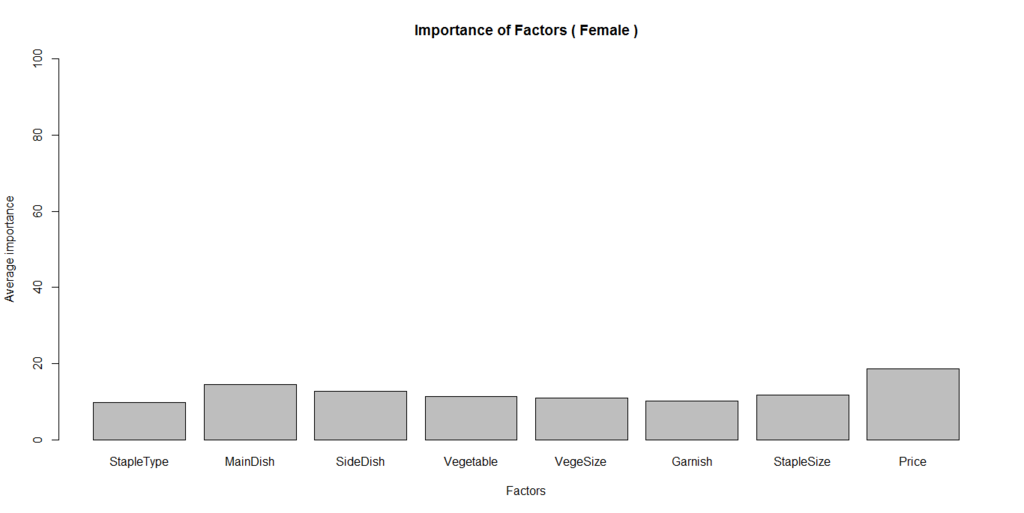
寄与率をみると、男女ともに、価格、メインのおかずの説明力が最も高い。また回帰係数の棒グラフから、係数の大きいものを選ぶと以下の組み合わせになった。

4.2 年齢別の分析
続いて、年齢別、弁当の購入頻度別に同様の分析を実施する。10代, 20代, 30代, 40代, 50代, 60代に分ける。ただし、サンプル数が20を下回る場合はモデルの精度を考慮して分析対象外とする。結果、30代, 40代のみが分析対象となる。
##Conjoint analysis by age segment
ages = c("Teenager", "Twenties", "Thirties", "Forties", "Fifties", "Sixties")
for (i in 1:max(dat$Age)) {
dat_p <- subset(dat, Age==i) #Extract each age segment from all data
if (nrow(dat_p) < 20) next #If number of rows is less than 20, skip the factor
dat_p <- dat_p[,-c(1:4)] #Delete demographic columns(ID, Sex, Age, Frequency)
Conjoint(dat_p, L18, attr) #Conjoint analysis
titleName = paste("Importance of Factors (", ages[i], ")")
title(main=titleName) #Add barplot title
Sys.sleep(5) #Stop program for 5 seconds
}
30代の寄与率の結果はこちら。
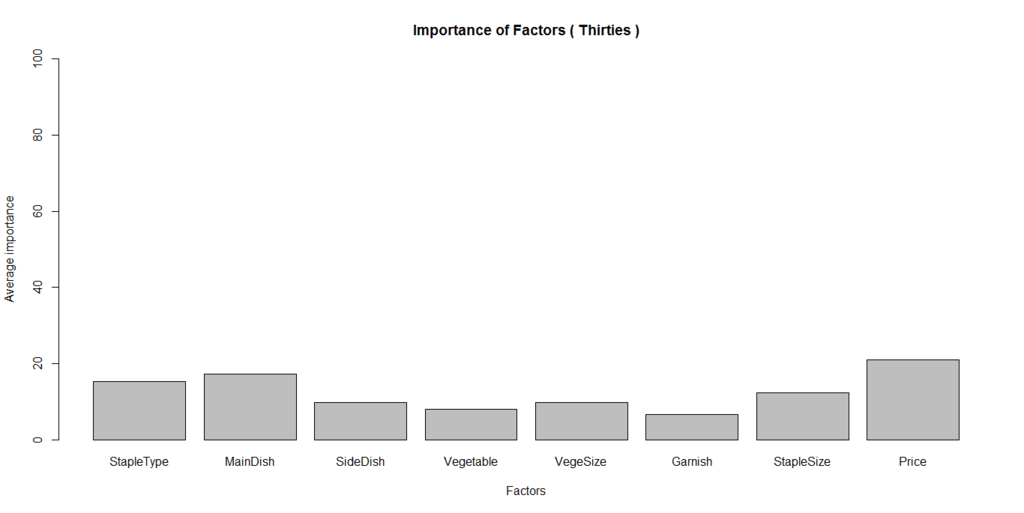
40代はこちら。
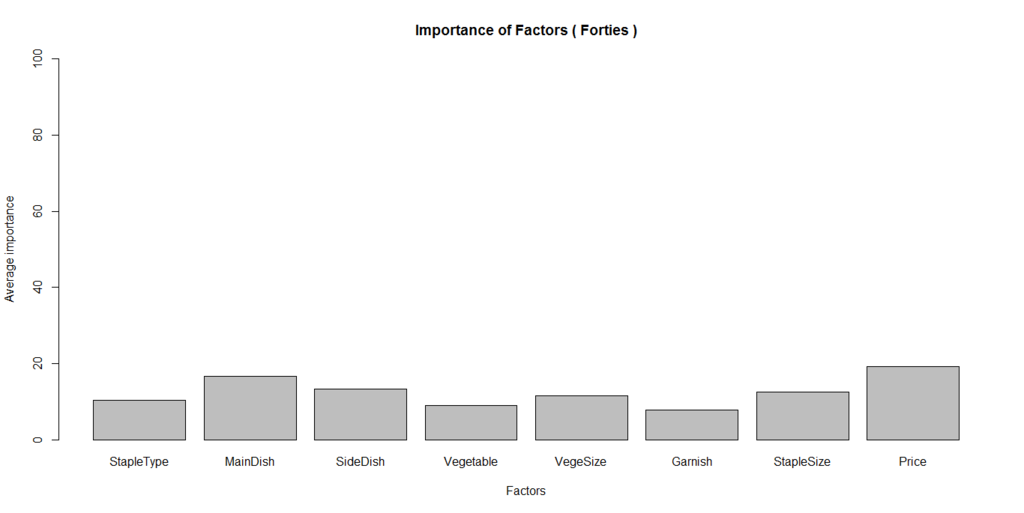
係数の棒グラフから割り出した、30代、40代向けに最適な組み合わせはこちら。

4.3 弁当の購入頻度別
弁当の購入頻度別で同様にコンジョイント分析を実施する。同様にサンプル数20未満のセグメントは除外する。結果、月に1回に買う人、月に1回未満の人に対して分析を実施することになる。
##Conjoint analysis by purchase frequency segment
freqs = c("everyday", "4-5 in a week", "2-3 in a week", "1 in a week", "2-3 in a month",
"1 in a month", "under 1 in a month")
for (i in 1:max(dat$Frequency)) {
dat_p <- subset(dat, Frequency==i) #Extract each frequency segment from all data
if (nrow(dat_p) < 20) next #If number of rows is less than 20, skip the factor
dat_p <- dat_p[,-c(1:4)] #Delete demographic columns(ID, Sex, Age, Frequency)
Conjoint(dat_p, L18, attr) #Conjoint analysis
titleName = paste("Importance of Factors (", freqs[i], ")")
title(main=titleName) #Add barplot title
Sys.sleep(5) #Stop program for 5 seconds
}
弁当を月1回買う人の寄与率の比較はこちら。
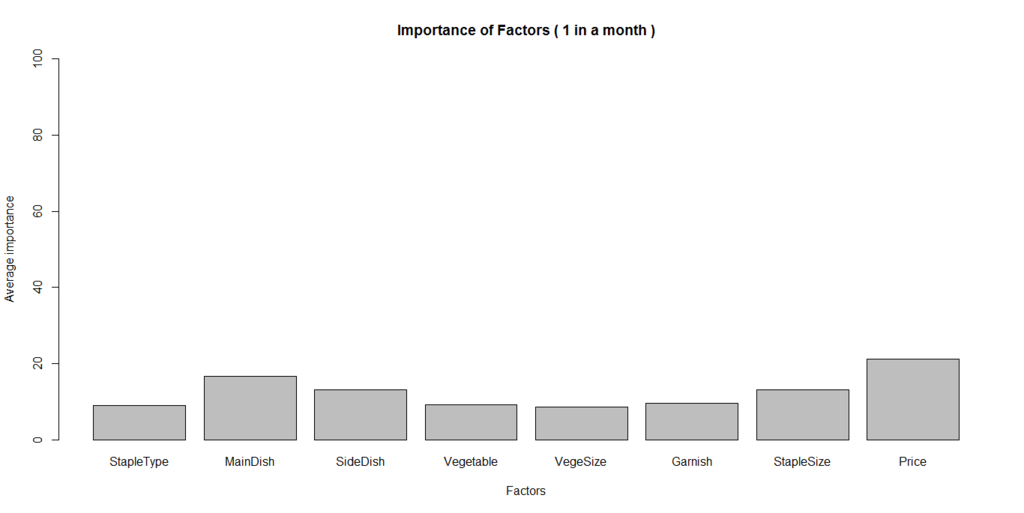
弁当を月に1回未満買う人の寄与率の比較はこちら。
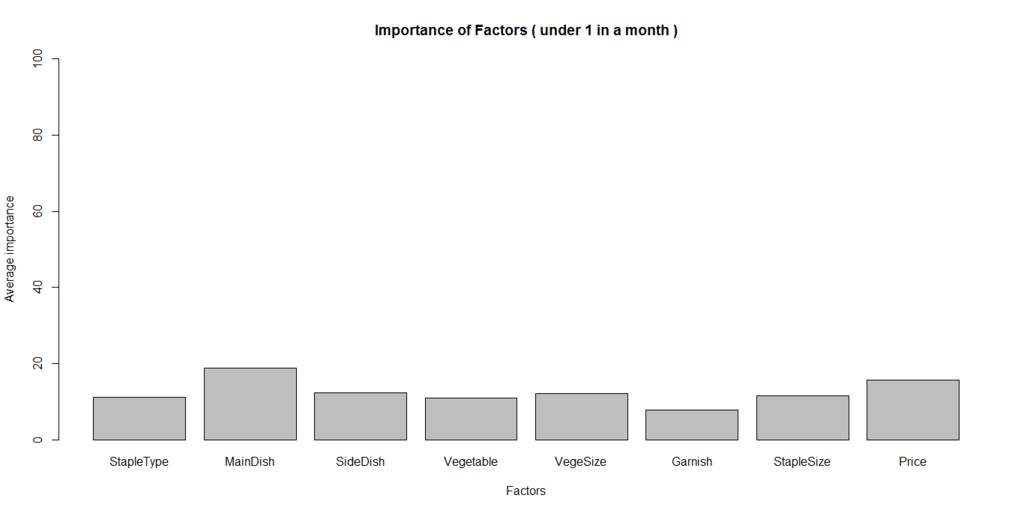
係数の棒グラフから割り出した、最適な組み合わせはこちら。

年代、購入頻度別にみても、値段とメインのおかずの説明力が最も高いことがわかる。また、どの年代、購入頻度、性別でも、野菜は玉ねぎ、値段は350円が最適であった。
5. まとめ
コンジョイント分析をすることで、限られた組み合わせから最適な組み合わせを抽出することができた。このように、一見組み合わせの数が膨大になりそうな場合も、コンジョイント分析を活用することで効率的に最適な組み合わせを抽出することができる。
















